marie theory

introduction

voici ce que les musiciens appellent le “cercle des quintes” :

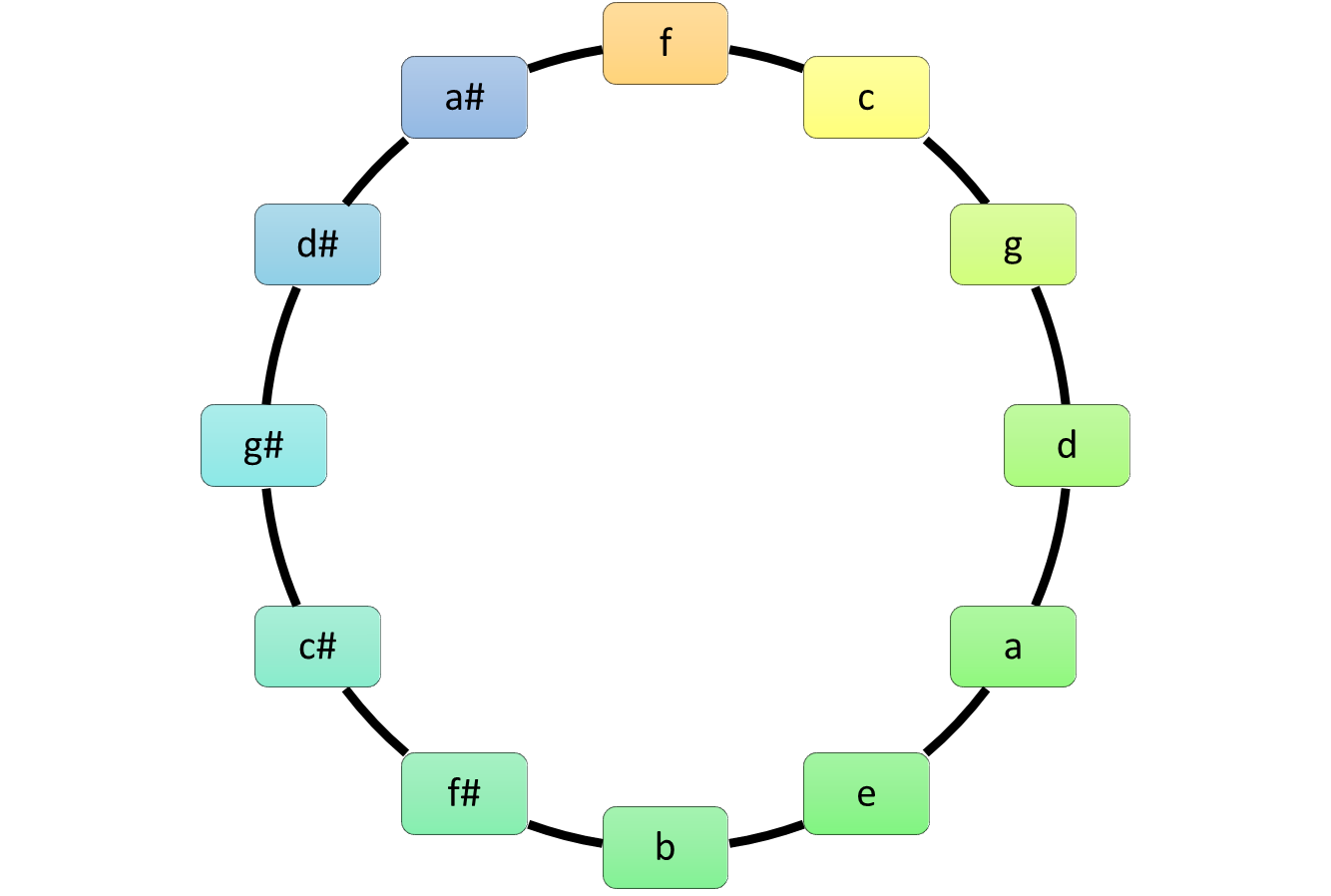
vous pouvez remarquer que les douze degrés de la gamme chromatique sont présents sont sur ce cercle. pour le dire autrement, à chaque note d’un piano correspond une case.

le cercle est ordonné de la façon suivante : en le parcourant dans le sens horaire, vous obtenez à chaque fois le degré qui est 5 demi-tons au-dessus du précedent.

l’utilité du cercle est de connaître immédiatement tous les accords d’une gamme.

mettons par exemple qu’on s’intéresse à la gamme de fa majeur. on vient écrire les chiffres 4 1 5 2 6 3 7 ainsi autour du cercle :

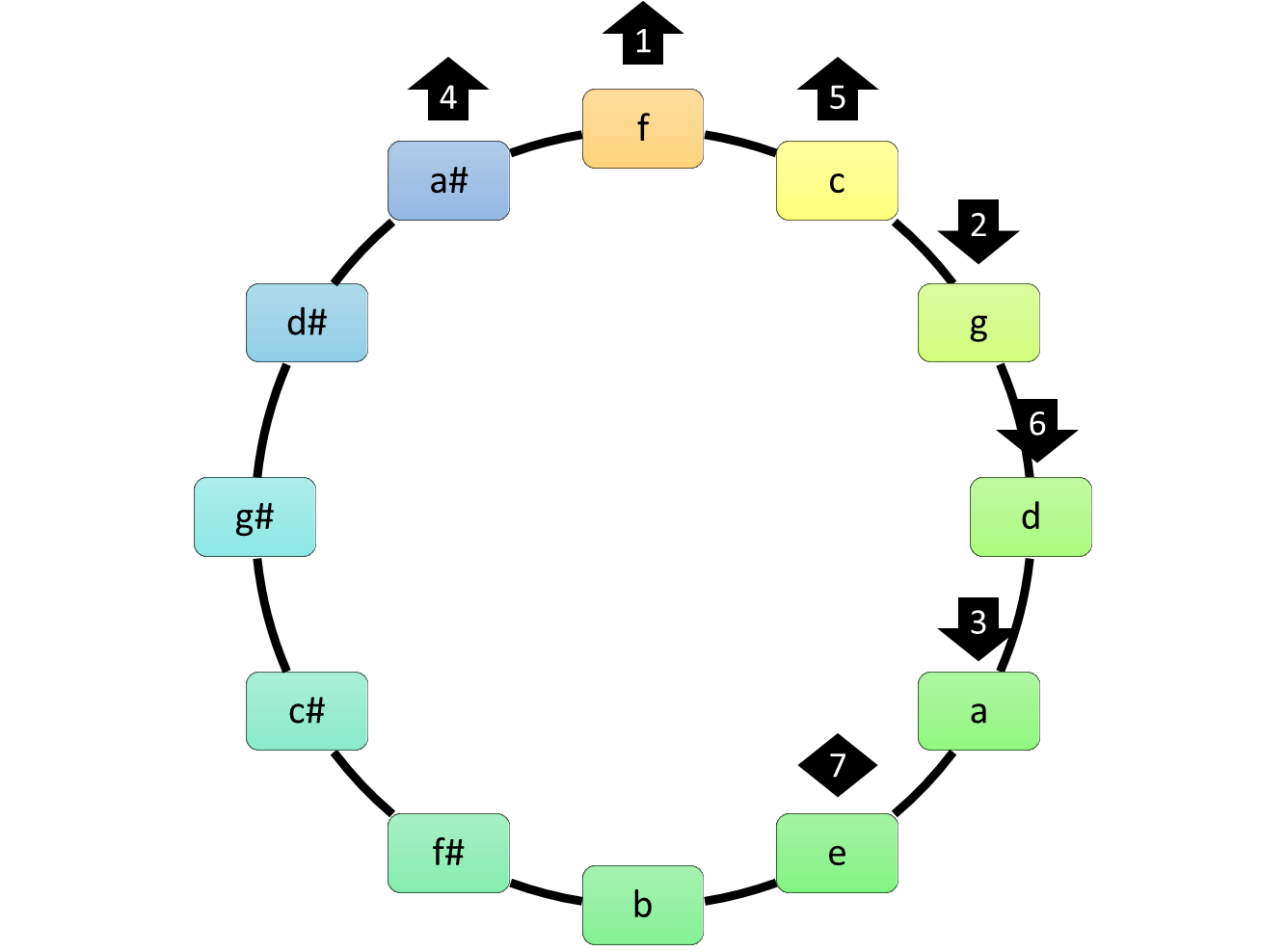
les flèches vers le haut correspondent aux accords majeurs sur la fondamentale, les flèches vers le bas aux accords mineurs, le losange à l’accord diminué.

et on obtient immédiatement les accords que l’on recherche.

pour une autre gamme, il suffit de faire “tourner” le cercle, comme un disque, jusqu’à mettre la fondamentale de la gamme recherché sous la flèche “1”.

pour faire la même chose avec une gamme mineure, il n’y a qu’à changer les indicateurs :

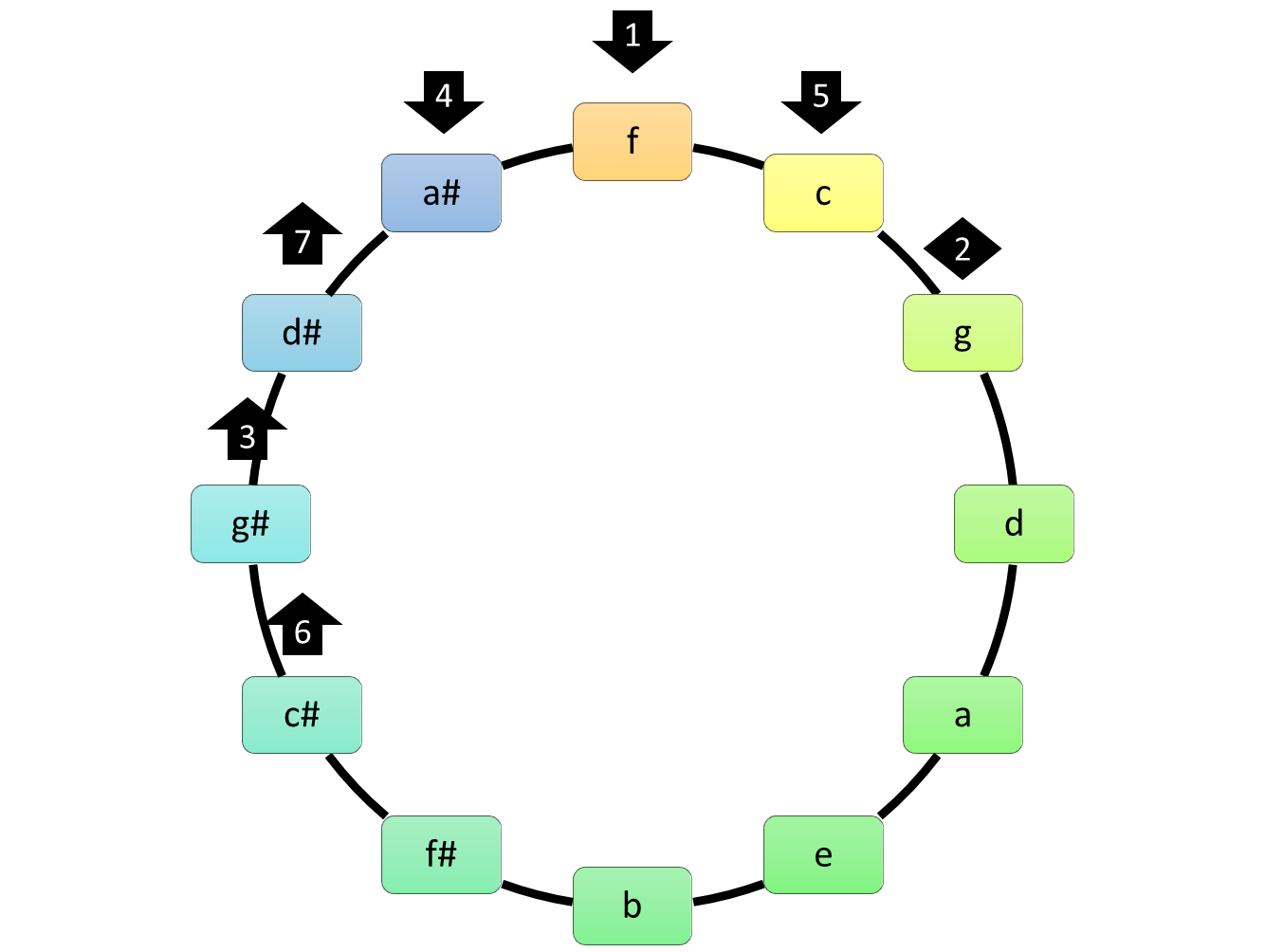
création

l’idée de la marie theory est de décomposer, de découper la lettre “m” en “i v i” (c’est plus facile à voir en majuscule).

pourquoi ? parce que.

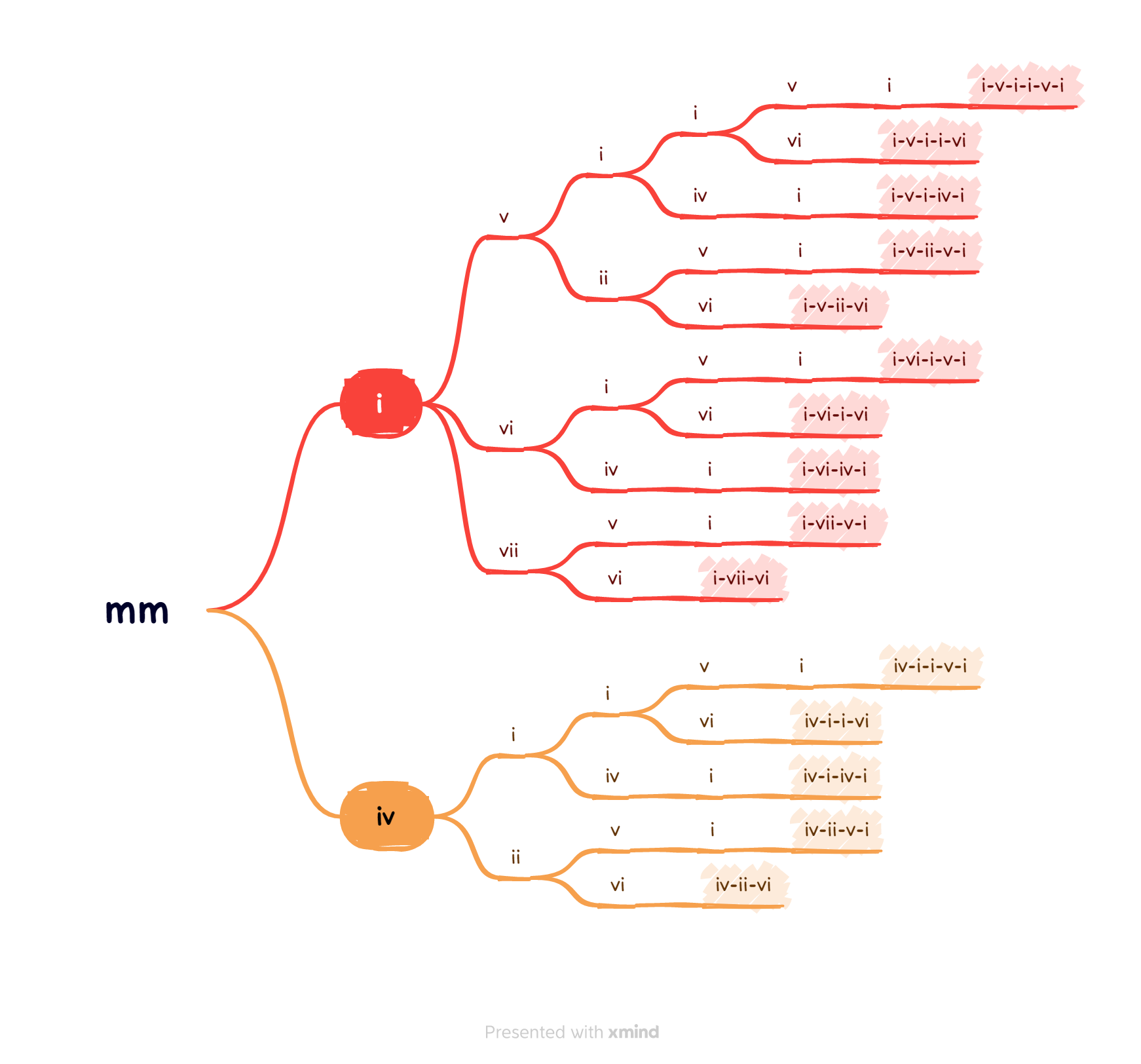
on va donc décomposer “mm” en “i v i i v i”.

on dénombre ensuite les regroupements faisables. un “v” par exemple peut se coller avec le “i” à sa droite pour former un “vi”. il peut ensuite, s’il y en a un, et s’il a envie, se coller avec le “i” encore à sa droite et donc former un “vii”.

il ne peut, en revanche, continuer à se coller à un éventuel “v” à sa droite, car “viiv” ne correspond pas à un chiffre romain de la gamme.

voici un schéma recensant tous ces découpages :

simplification

regroupons-les par longueur dans un tableau :

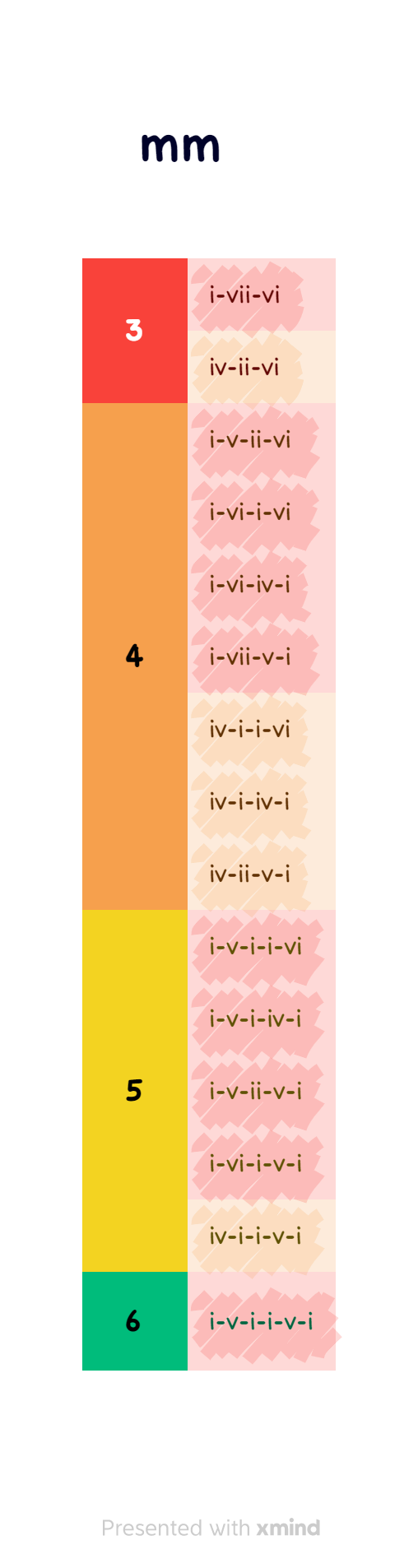
effaçons les répétitions (i-vi-i-vi peut devenir i-vi) ainsi que ceux semblables par permutation circulaire (eg. i-vi-iv-i = iv-i-i-vi).

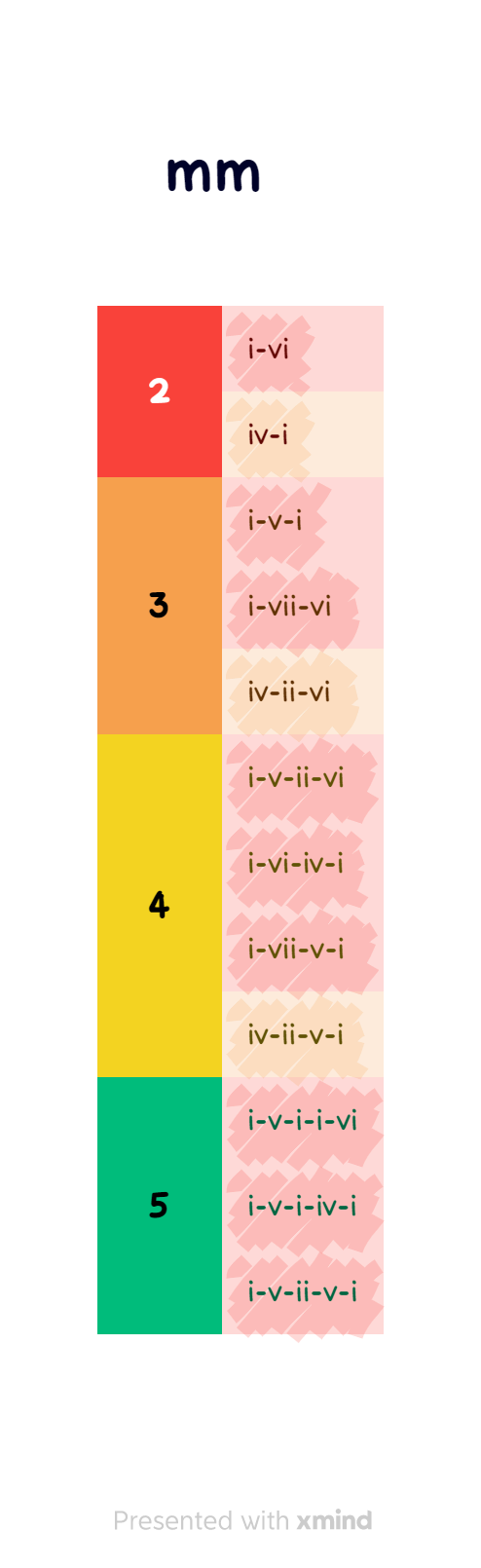
voici.

fait amusant : ils étaient douze. un petit rigolo pourrait les arranger sur le modèle du cercle des quintes. s’il voulait.

esthétisation

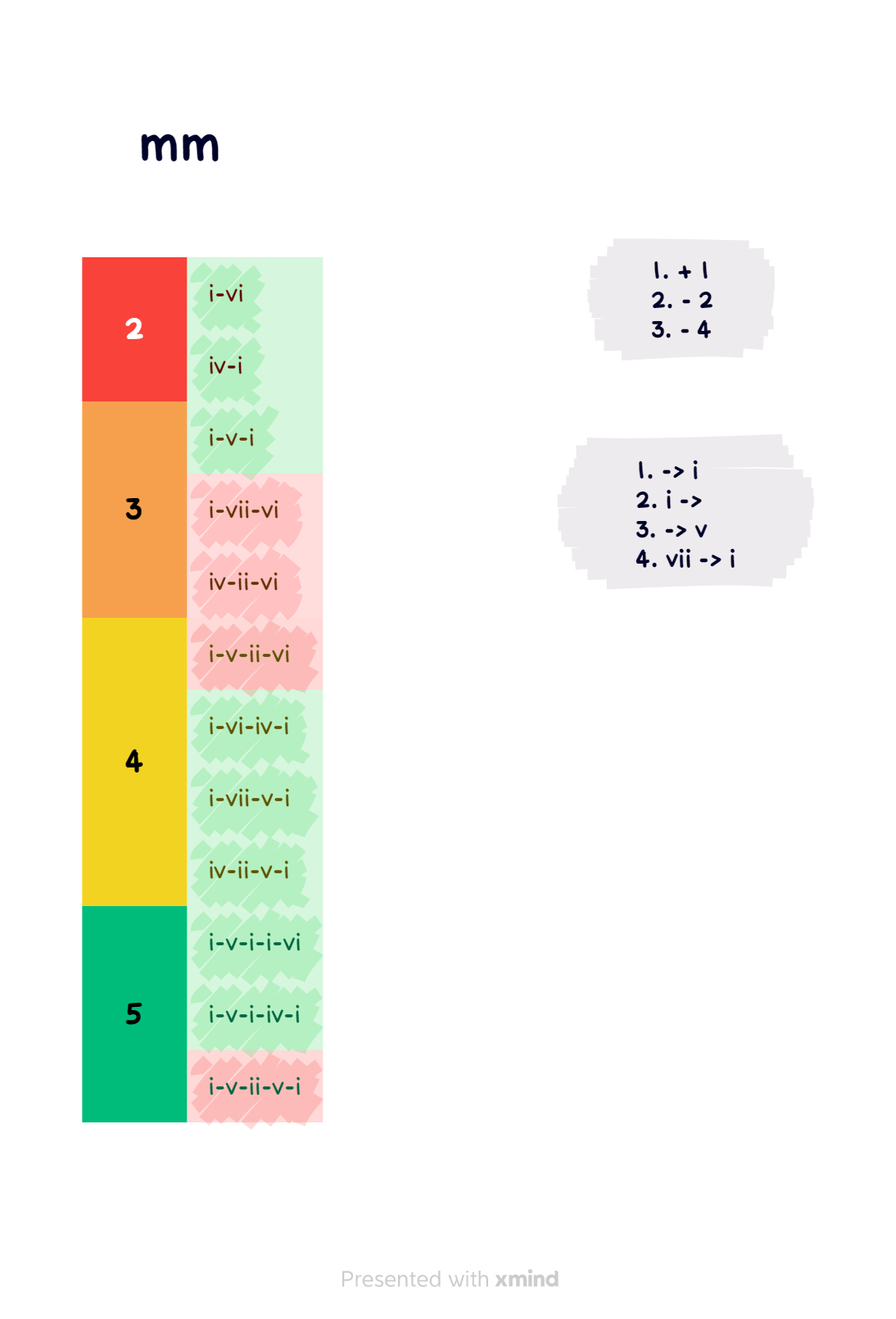
nous allons rajouter deux ensembles de règles. ce sont des règles “esthétiques” : l’objectif est d’arriver à un résultat écoutable par des esprits sans imagination.

premier ensemble : le mouvement de la fondamentale. elle ne peut que monter d’un cran sur la gamme (+ 1), descendre de deux crans (-2) ou de quatre crans (-4).

deuxième ensemble : quelques propriétés des degrés.

• n’importe quel accord peut revenir sur le i (-> i)
• le i peut aller sur n’importe quel accord (i ->)
• n’importe quel accord peut revenir sur le v (-> v)
• le vii doit revenir sur le i (vii -> i)

en vert, les progressions qui respectent ces deux ensembles :

programmation

générons quelque chose.

voici un code qui choisit un accord au hasard, une progression au hasard, et imprime les accords à jouer.

from itertools import cycle
from random import choice

progs = {
    2: [
        "i-vi".split("-"),
        "iv-i".split("-"),
    ],
    3: [
        "i-v-i".split("-"),
        "i-vii-vi".split("-"),
        "iv-ii-vi".split("-"),
    ],    
    4: [
        "i-v-ii-vi".split("-"),
        "i-vi-iv-i".split("-"),
        "i-vii-v-i".split("-"),
        "iv-ii-v-i".split("-"),
    ],    
    5: [
        "i-v-i-i-vi".split("-"),
        "i-v-i-iv-i".split("-"),
        "i-v-ii-v-i".split("-"),
    ],
}

roots = "f_c_g_d_a_e_b_f#_c#_g#_d#_a#".split("_")
circle = cycle(roots)

def get_chords(root='f', mode='major'):
    while next(circle) is not root:
        pass
    degrees = {}
    if mode == 'major':
        degrees['i'] = root
        degrees['v'] = next(circle)
        degrees['ii'] = next(circle) + "m"
        degrees['vi'] = next(circle) + "m"
        degrees['iii'] = next(circle) + "m"
        degrees['vii'] = next(circle) + "°"
        for _ in range(5):
            next(circle)
        degrees['iv'] = next(circle)
    elif mode == 'minor':
        degrees['i'] = root + "m"
        degrees['v'] = next(circle) + "m"
        degrees['ii'] = next(circle) + "°"
        for _ in range(5):
            next(circle)
        degrees['vi'] = next(circle)
        degrees['iii'] = next(circle)
        degrees['vii'] = next(circle)
        degrees['iv'] = next(circle) + "m"    
    return degrees
    
    
root = choice(roots)
mode = choice(['major', 'minor'])
degrees = get_chords(root=root, mode=mode)

prog_size = choice([*progs.keys()])
prog = choice(progs[prog_size])

print("key", degrees['i'])
print("prog", prog)
print("---")
for degree in prog:
    chord = degrees[degree]
    print(chord)

donne par exemple

key cm
prog ['i', 'vi', 'iv', 'i']
---
cm
g#
fm
cm

on pourrait raffiner. par exemple, mettre les v et vii majeurs lorsque l’accord est mineur (raffinement harmonique). on pourrait.

composition

comment écouter maintenant.

si vous voulez continuer en python, il existe des librairies.

vous pouvez aussi coder votre propre synth comme un pur malade.

vous pouvez écrire du midi et l’envoyer vers un daw.

vous pouvez sortir le piano ou la clarinette.

vous m’en direz des nouvelles.