marie theory 2
voyons voyons voyons.
il y a 39 916 800 (11!) façons de répartir les progressions d’accord de la marie theory.
il va falloir élaguer.
le cercle des quintes classiques a la propriété suivante : plus les accords sont proches, plus ils partagent de notes dans leurs gammes.
nous proposons donc, pour chaque configuration possible, compter les accords en commun entre les progressions adjacentes : (i-vi et iv-i = 1, i-v-i-i-vi et i-v-i-iv-i = 4).
le score maximal pouvant être atteint est 30, auquel correspond encore 350 configurations.
les critères suivants sont esthétiques.
sur les 350, seules 4 ont les progressions i-vi et iv-i diamétralement opposées.
sur les 4, 2 sont mieux équilibrées par rapport aux longueurs des progressions.
les 2 restants sont le même cercle parcouru dans les deux sens.
l’un semble avoir un meilleur iv-v-i (voir iv-i-v-ii) que l’autre.
nous obtenons enfin notre méta-cercle :
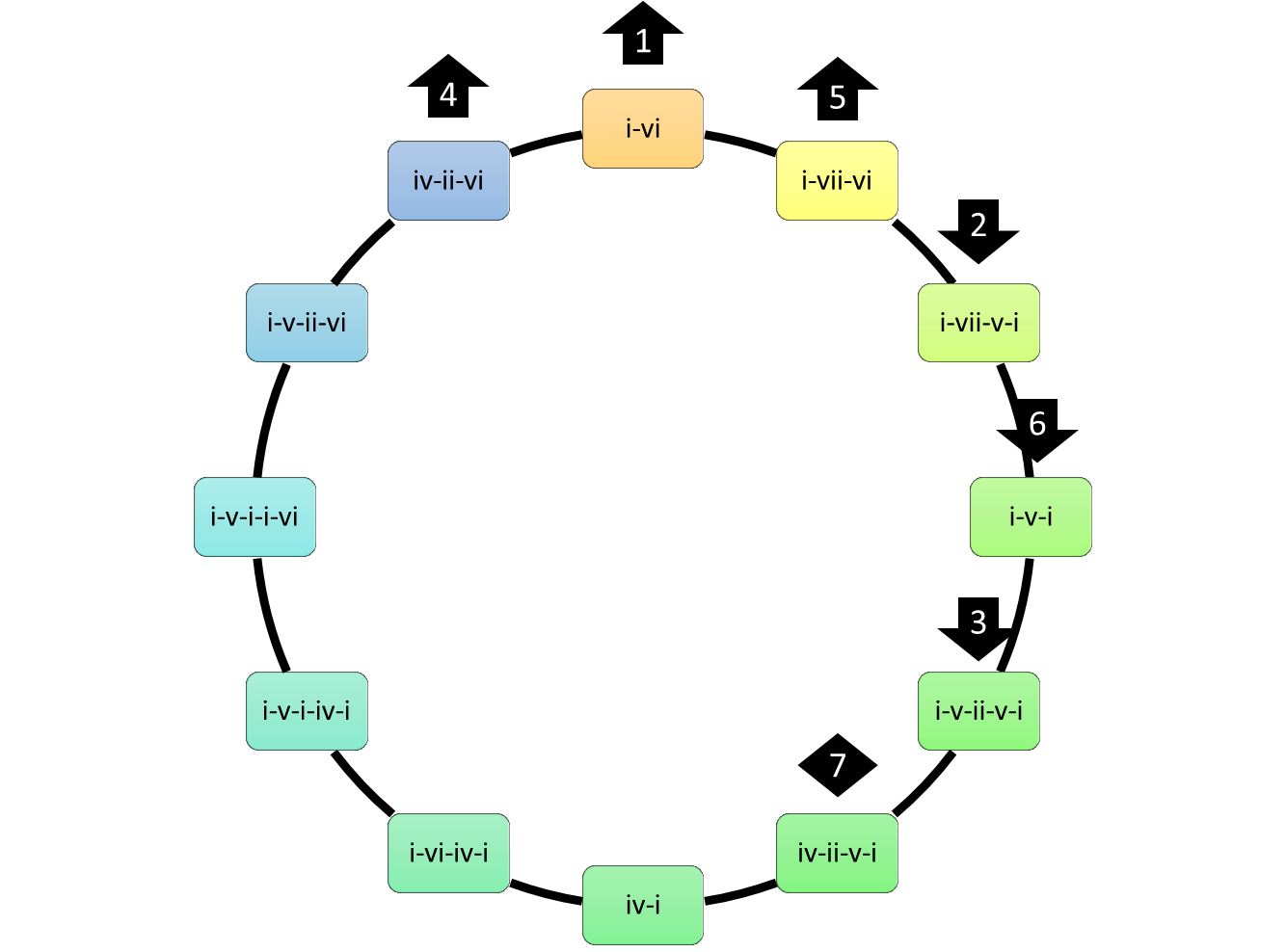
en mineur :
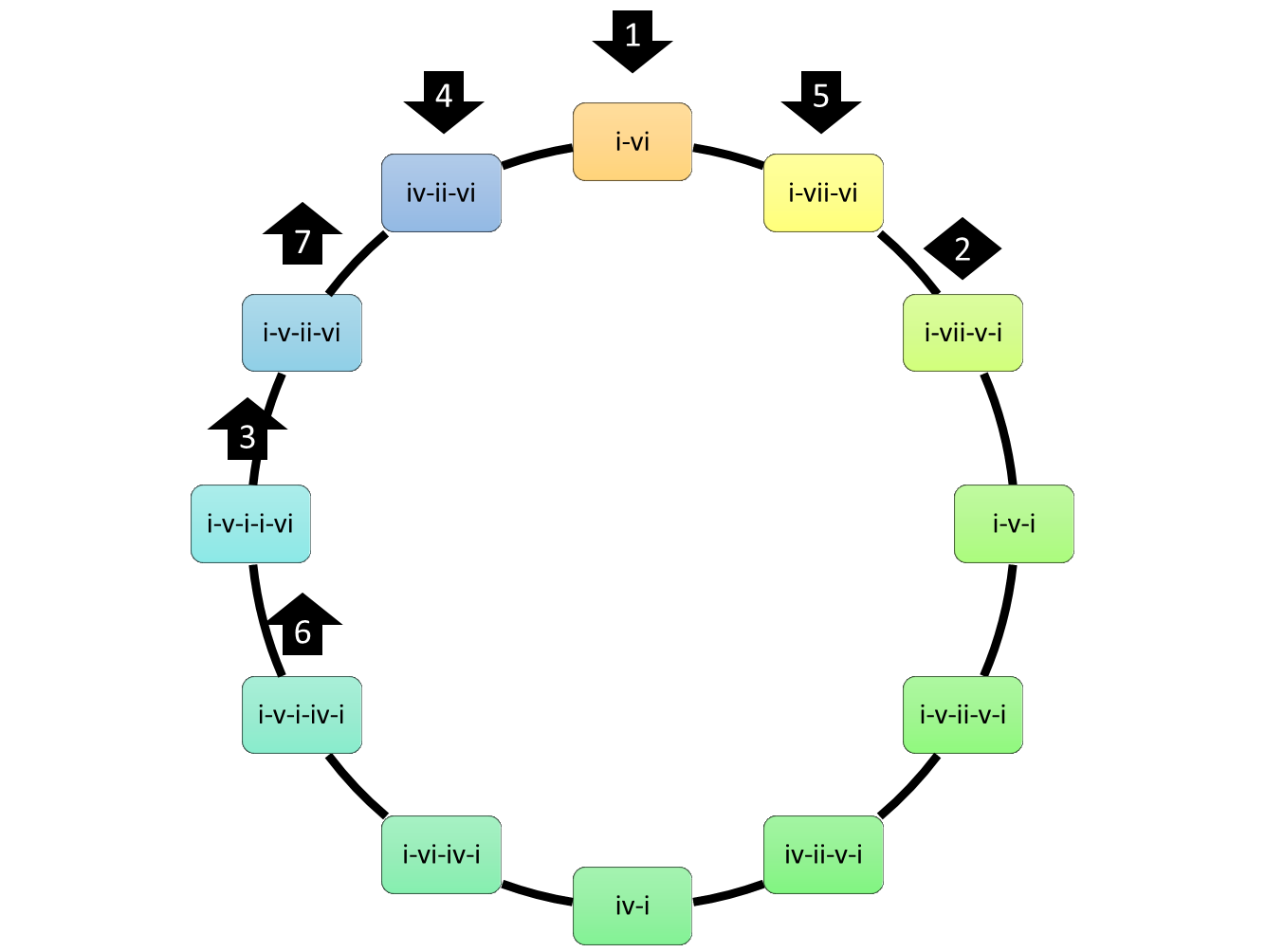
programmation
avec 1 choix sur 24 pour l’accord de départ, 1 choix sur 12 pour la progression de départ, et 1 choix sur 12 pour la métaprogression, nous obtenons 3456 suites d’accord possibles, et c’est joli.
voici le code :
from itertools import cycle
from random import choice
roots = ['f', 'c', 'g', 'd', 'a', 'e', 'b', 'f#', 'c#', 'g#', 'd#', 'a#']
progs = ['i vi', 'i vii vi', 'i vii v i', 'i v i', 'i v ii v i', 'iv ii v i', 'iv i', 'i vi iv i', 'i v i iv i', 'i v i i vi', 'i v ii vi', 'iv ii vi']
circle = cycle(roots)
metacircle = cycle(progs)
def get_degrees(start, mode, meta=False):
_circle = metacircle if meta else circle
while next(_circle) is not start:
pass
degrees = {}
if mode == 'major':
degrees['i'] = start
degrees['v'] = next(_circle)
degrees['ii'] = next(_circle) + "m "[meta]
degrees['vi'] = next(_circle) + "m "[meta]
degrees['iii'] = next(_circle) + "m "[meta]
degrees['vii'] = next(_circle) + "° "[meta]
for _ in range(5):
next(_circle)
degrees['iv'] = next(_circle)
elif mode == 'minor':
degrees['i'] = start + "m "[meta]
degrees['v'] = next(_circle) + "m "[meta]
degrees['ii'] = next(_circle) + "° "[meta]
for _ in range(5):
next(_circle)
degrees['vi'] = next(_circle)
degrees['iii'] = next(_circle)
degrees['vii'] = next(_circle)
degrees['iv'] = next(_circle) + "m "[meta]
return degrees
root = choice(roots)
mode = choice(['major', 'minor'])
metaprog = choice(progs)
prog = choice(progs)
degrees = get_degrees(start=root, mode=mode)
metaprogs = get_degrees(start=prog, mode=mode, meta=True)
print("mode", mode)
print("metaprog", metaprog)
print("prog", prog)
print("key", degrees['i'])
print("---")
for metadegree in metaprog.split():
prog = metaprogs[metadegree]
for degree in prog.split():
chord = degrees[degree]
print(chord, end=" - ")
print()
voici le premier résultat que j’obtiens :
mode minor
metaprog i vii vi
prog iv ii v i
key bm
---
em - c#° - f#m - bm -
bm - f#m - bm -
bm - a - g -
c’est bieng. voilà ce que ça peut donner.
protip : si l’accord est trop compliqué à amener, avant d’amener des accords de transition, essayer d’abord une astuce simple.
regardez les altérations amenées par la gamme de l’accord en question par rapport à la clé. vous pouvez utiliser n’importe quel accord qui contient ces altérations.